Сортировка массивов
Сортировка массивов
Под сортировкой понимается процесс перестановки элементов некоторого множества в порядке убывания или возрастания. Если элементы множества — скаляры, то сортировка ведется относительно их значений. Если элементы множества — структуры, то каждая структура должна иметь поле, относительно которого будет производиться упорядочивание местоположения элементов (то есть сортировка) относительно других элементов-структур множества.
Различают два типа алгоритмов сортировки: сортировку массивов и сортировку файлов. Другое их название — алгоритмы внутренней и внешней сортировки. Разница заключается в местонахождении объектов сортировки: для внутренней сортировки — это оперативная память компьютера, для внешней — файл. В данном разделе будут рассмотрены алгоритмы внутренней сортировки массивов. Алгоритмы внешней сортировки будут рассмотрены в разделе, посвященном работе с файлами.
Существует несколько алгоритмов сортировки массивов, которым следует уделить внимание в контексте проблемы изучения ассемблера. По критерию эффективности алгоритмы сортировки массивов делят на простые и улучшенные. Среди простых методов сортировки, которые также называют сортировками «на том же месте», мы рассмотрим следующие:
Улучшенные методы сортировки в нашем изложении будут представлены следующими алгоритмами:
Сортировка прямым включением
Идея сортировки прямым включением (программа prg4_96.asm) заключается в том, что в сортируемой последовательности masi длиной n (i = 0..n - 1) последовательно выбираются элементы начиная со второго (i< 1) и ищутся их местоположения в уже отсортированной левой части последовательности. При этом поиск места включения очередного элемента х в левой части последовательности mas может закончиться двумя ситуациями:
Первая ситуация разрешается тем, что последовательность mas начиная с masi раздвигается в правую сторону и на место masi перемещается х. Во второй ситуации следует сместить всю последовательность вправо и на место mas0 переместить х.
В этом алгоритме для отслеживания условия окончания просмотра влево отсортированной последовательности используется прием «барьера». Суть его в том, что к исходной последовательности слева добавляется фиктивный элемент X. В начале каждого шага просмотра влево отсортированной части массива элемент X устанавливается в значение того элемента, для которого будет осуществляться поиск места вставки.
ПРОГРАММА рrg4_96
//prg4_96 - программа на псевдоязыке сортировки прямым включением //Вход: mas[n] - неупорядоченная последовательность байтовых двоичных значений. //Выход: mas[n] - упорядоченная последовательность байтовых двоичных значений. //.---------...----...--.........
ПЕРЕМЕННЫЕ
INT_BYTE n=8: //количество элементов в сортируемом массиве
INT_BYTE mas[n]: //сортируемый массив размерностью п (О..п-l)
INT_BYTE X; //барьер
INT_BYTE i=0: j=0 //индексы
НАЧ_ПРОГ
ДЛЯ 1:-1 ДО п-1 /Л изменяется в диапазоне О..п-l
НАЧ_БЛ0К_1
//присвоение исходных значений для очередного шага
X:=mas[i]: mas[0]:=X; j:=i-l
ПОКА (X<mas[j]) ДЕЛАТЬ НАЧ_БЛОК_2
mas[j+l]:=mas[j]; j:=j-l КОН_БЛ0К_2
mas[j+l]:=X
КОН_БЛОК_1 КОН_ПРОГ
;prg4_96.asm - программа на ассемблере сортировки прямым включением.
.data
mas db 44,55.12.42.94.18.06.67 :задаем массив
n=$-mas
X db 0 :барьер
.code
mov ex.п-1 :цикл по 1
movsi.l :i=2 сус13: присвоение исходных значений для очередного шага
mov al ,mas[si]
movx.al :X: = mas[i]: mas[0]:-X: j:=i-l
push si ;временно сохраним i. теперь J-1 :еще один цикл, который перебирает элементы до барьера x=mas[i] сус12: mov al,mas[si-l]
emp x,al ;сравнить х < mas[j-l]
ja ml :если x > mas[j-l] : если x < mas[j-l]. то
mov al,mas[si-l]
irovmas[si],al
dec si
jmpcycl2 ml: mov al ,x
movmas[si].al
pop si
incsi
loop cyc!3
Этот способ сортировки не очень экономен, хотя логически он выглядит очень естественно.
Сортировка прямым выбором
В алгоритме сортировки прямым выбором (программа prg4_99.asm) на каждом шаге просмотру подвергается несортированная правая часть массива. В ней ищется очередной минимальный элемент. Если он найден, то производится его перемещение на место крайнего левого элемента несортированной правой части массива.
ПРОГРАММА prg4_99
//prg4_99 - программа на псевдоязыке сортировки прямым выбором //Вход: mas[n] - неупорядоченная последовательность байтовых двоичных значений. //Выход: mas[n] - упорядоченная последовательность байтовых двоичных значений. // .
ПЕРЕМЕННЫЕ
INT_BYTE n=8; //количество элементов в сортируемом массиве INT_BYTE mas[n]; //сортируемый массив размерностью п (О..п-l) INTJYTE X: i=0: j=0: k=0 // i. j, k - индексы НАЧ_ПРОГ
ДЛЯ i:=l ДО n-1 //i изменяется в диапазоне 1..П-1 НАЧ_6ЛОК_1
//присвоение исходных значений для очередного шага k:=i: Х: = raas[i]
ДЛЯ j:-1+l ДО n //j изменяется в диапазоне 1+1..п ЕСЛИ mas[j]<X TO НАЧ_БЛ0К_2
k:=j: x:= mas[j] К0Н_БЛ0К_2
mas[k]:= mas[i]; mas[i]:=X КОН_БЛОК_1 КОН_ПРОГ
;prg4_99.asm - программа на ассемблере сортировки прямым выбором.
.data
masdb 44.55.12,42,94,18.06,67 ;задаем массив
n-$-mas
X db 0
К dw 0
.code
:внешний цикл - по 1
mov сх.л-1
mov si ,0 cycll: push ex
mov k.si :k:=i
mov al ,mas[si]
movx.al ;x:=mas[i]
push si :временно сохраним i - теперь j=I+l
incsi :j=I+l
сложенный цикл - по j
mov al ,n
sub ax.si
mov ex,ax количество повторений внутреннего цикла по j cycl2: mov al ,mas[si]
cmpal ,x
ja ml
mov k.si ;k:=j
moval ,mas[si]
movx.al :x:=mas[k] ml: inc si :j:=j+l
loop cycl2
pop si
mov al ,mas[s1]
movdi Л
mov mas[di],al :mas[k]:=mas[i]
mov al,x
mov mas[si],al :mas[i]:-x
inc si
pop ex
loop cycll
Первый вариант сортировки прямым обменом
Этот метод основан на сравнении и обмене пар соседних элементов до их полного упорядочивания (программа prg4_101.asm). В народе этот метод называется методом пузырьковой сортировки. Действительно, если упорядочиваемую последовательность расположить не слева направо, а сверху вниз («слева» — это «верх»), то визуально каждый шаг сортировки будет напоминать всплытие легких (меньших по значению) пузырьков вверх.
ПРОГРАММА prg4_101
//..
//prg4_101 - программа на псевдоязыке сортировки прямым обменом 1
//Вход: mas[n] - неупорядоченная последовательность байтовых двоичных значений.
//Выход: mas[n] - упорядоченная последовательность байтовых двоичных значений.
//....-..
ПЕРЕМЕННЫЕ
INTJ3YTE n=8: //количество элементов в сортируемом массиве INT_BYTE mas[n]; //сортируемый массив размерностью п (О..п-l) INTJYTE X: i-0; j-0 // i. j - индексы НАЧ_ПРОГ
ДЛЯ i:=l ДО n-1 //i изменяется в диапазоне L.n-l НАЧ_БЛ0К_1
ДЛЯ j:=n-l ДОВНИЗ i //j изменяется в диапазоне 1+1.,П ЕСЛИ mas[j-l]< mas[j] TO НАЧ_БЛОК_2
x:=mas[j-l]; mas[j-l]:=mas[j]: mas[j]:=X К0Н_БЛ0К_'2 К0Н_БЛ0К_1 КОН_ПРОГ
;prg4_101.asm - программа на ассемблере сортировки прямым выбором 1.
ПОВТОРИТЬ
.data ДЛЯ j:=r ДОВНИЗ 1 //j изменяв!
: задаем массив ЕСЛИ mas[j-l]< mas[j] TO
masdb 44,55.12,42.94.18.06,67 НАЧ^БЛОК_1
n=$-mas x:=mas[j-l]: mas[j-l]:
X db 0 КОН БЛОК 1
ДЛЯ j:-l ДОВНИЗ г //j изменяв"
.code ЕСЛИ mas[j-l]< mas[j] TO
НАЧ_БЛОК_2
;внешний цикл - по 1 x:=mas[j-l]: mas[j-l]:
mov ex, n -1 КОН БЛОК 2
mov si .1 r:=k-l
cycl1: ПОКА (1>г)
push ex КОН_ПРОГ
mov ex n
1 1 1\щ/ V \— Г\ , 1 1 sub ex,si количество повторений внутреннего цикла :prg4 104.asm - программа на аса
push si временно сохраним i - теперь j=n mov si ,n-l
cycl2: :ЕСЛИ mas[j-l]< mas[j] TO .data
mov al ,mas[si-l] :задаем массив
cmpmas[si].al masdb 44.55,12.42.94.18.06.67
ja ml n=$-mas
movx.al :x=mas[j-l] X db 0
mov al ,mas[si] L dw 1
mov mas[si-l],al ;mas[j-l]= mas[j] R dw n
mov al,x k dw n
mov mas[si].al :mas[j]=x
ml: dec si :цикл по j с декрементом n-i раз .code
loop cycl2 ;.... :1:=2: г:=n: k: =n
pop si cycl3: :ДЛЯ j:-r ДОВНИЗ 1
inc si mov si .R : j:=R
pop ex push si
loop cycll sub si.L
;.... mov ex,si количество по
pop si
Второй вариант сортировки прямым обменом
Эту сортировку называют шейкерной (программа prg4_104.asm). Она представляет собой вариант пузырьковой сортировки и предназначена для случая, когда последовательность почти упорядочена. Отличие шейкерной сортировки от пу зырьковой в том, что на каждой итерации меняется направление очередного про хода: слева направо, справа налево.
ПРОГРАММА prg4_104 mov mas[si-l].al :mas[j-
mov al ,x
//prg4_104 - программа на псевдоязыке сортировки прямым обменом 2 (шейкерной) mov mas[si].al ;mas[j]:-x
//Вход: mas[n] - неупорядоченная последовательность байтовых двоичных значений. mov k.si :k:=j
//Выход: mas[n] -упорядоченная последовательность байтовых двоичных значений. ml: dec si :j:=j-l
loop cycll
ПЕРЕМЕННЫЕ mov ax.k
INT BYTE n=8: //количество элементов в сортируемом массиве inc ax
INT BYTE mas[n]: //сортируемый массив размерностью п (О..п-l) mov Lax :L:=k+l
INT BYTE X: 1-0; j=0: г=0: 1=0: k=0 // i. j. г. 1. k - индексы : цикл cycl2 :ДЛЯ j:=l ДОВНИЗ
НАЧ_ПРОГ mov si.L :j:=L
1:=2: r:=n; k:=n mov ax.R
ПОВТОРИТЬ
ДЛЯ j:=r ДОВНИЗ 1 //j изменяется от 1 до г ЕСЛИ mas[j-l]< mas[j] TO НАЧ_БЛОК_1
x:=mas[j-l]: mas[j-l]:=mas[j]: mas[j]:=X: k:=j КОН_БЛОК_1
ДЛЯ j:=l ДОВНИЗ г //j изменяется от г до 1 ЕСЛИ mas[j-l]< mas[j] TO НАЧ_БЛОК_2
x:-mas[j-l]; mas[j-l]:=mas[j]; mas[j]:=X; k:=j К0Н_БЛ0К_2 r:=k-l ПОКА (1>г) КОН_ПРОГ
:prg4_104.asm - программа на ассемблере сортировки прямым выбором 2 (шейкерной).
.data
: задаем массив
masdb 44.55.12.42.94.18.06.67
n=$-mas
X db 0
L dw 1
R dw n
k dw n
.code
;.... :1:=2: r:=n: k:=n
cycl3: :ДЛЯ ДОВНИЗ 1
mov si.R :j:=R
push si
sub si.L
mov ex,si количество повторений цикла cycll
pop si
dec si cycll: :ЕСЛИ mas[j-l]< mas[j] TO
mov al,mas[si-1]
emp al.mas[si]
jna ml
mov al,mas[si-1]
mov x.al ;x:=mas[j-l]
mov al.mas[si]
mov mas[si-l].al :mas[j-l]:=mas[j]
mov a 1, x
mov mas[si].al :mas[j]:=x
mov k.si ;k:=j
ml: dec si :j:=j -1
loop cycll
mov ax.k
inc ax
mov L.ax :L:=k+l : цикл сус12 :ДЛЯ j:-l ДОВНИЗ г
mov si.L :j:=L
mov ax.R
sub ax.L
mov ex.ax количество повторений цикла сус12
cyc12: mov al.mas[si-l] :ЕСЛИ mas[j-l]< mas[j] TO
emp al.mas[si]
jna m2
mov al,mas[si-l]
mov x.al ;x:=mas[j-l]
mov al.mas[si]
mov mas[si-l].al ;mas[j-l]:=mas[j]
mov al .x
mov mas[si].al :mas[j]:=x
mov k.s1 :k:=j
m2: inc si :j:=j+l
loop cycl2
mov ax.k
dec ax
mov R.ax :R:=k-1
emp L.ax ;L>R - ?
jae $+5
jmp cycl3
Улучшение классических методов сортировки
Приведенные выше четыре метода сортировки — базовые. Их обычно рассматривают как основу для последующего обсуждения и совершенствования. Ниже мы рассмотрим несколько усовершенствованных методов сортировки, после чего вы сможете оценить эффективность их всех.
Сортировка Шелла
Приводимый ниже алгоритм сортировки (программа prg4_107.asm) носит имя автора, который предложил его в 1959 году. Суть его состоит в том, что сортировке подвергаются не все подряд элементы последовательности, а только отстоящие друг от друга на определенном расстоянии h. На каждом шаге значение h изменяется, пока не станет (обязательно) равно 1. Важно правильно подобрать значения h для каждого шага. От этого зависит скорость работы алгоритма. В качестве значений h могут быть следующие числовые последовательности: (4, 2, 1), (8, 4, 2, 1) и даже (7, 5, 3, 1). Последовательности чисел можно вычислять аналитически. Так, Кнут предлагает следующие соотношения:
Подобное аналитическое получение последовательности смещений дает возможность разрабатывать программу, которая динамически подстраивается под конкретный сортируемый массив.
Отметим, что если h=1, то алгоритм сортировки Шелла вырождается в сортировку прямыми включениями.
Существует несколько вариантов алгоритма данной сортировки. Вариант, рассмотренный ниже, основывается на алгоритме, предложенном Кнутом.
ПРОГРАММА prg4_107
//prg4_107 - программа на псевдоязыке сортировки Шелла
//Вход: mas_dist=(7,5,3.1) - массив смещений: mas[n] - неупорядоченная
последовательность байтовых двоичных значений. //Выход: mas[n] -упорядоченная последовательность байтовых двоичных значений.
-ПЕРЕМЕННЫЕ
INT_BYTE t=4; //количество элементов в массиве смещений
INT_BYTE mas[n]; //сортируемый массив размерностью п (О..п-1)
INT_BYTE mas_dist[t]=(7.5,3,l): // массив смещений размерностью t (O..t-1)
INT_BYTE h=0 //очередное смещение из mas_dist[]
INT_BYTE X: i=0: j-0; s=0 // i. j. s - индексы
НАЧ_ПРОГ
ДЛЯ s:=0 ДО t-1 НАЧ_БЛОК_1
h:=mas_dist[s] ДЛЯ j:4i ДО n-1 НАЧ_БЛ0К_2
i:=j-h: X:=mas[i]
@@d4: ЕСЛИ Х>= mas[i] TO ПЕРЕЙТИ_НА №66 mas[i+h]:=mas[i]: i:=i-h ЕСЛИ 1>0 ТО ЛЕРЕЙТИ__НА @@d4 Ш6: mas[i+h]:=x К0Н_БЛ0К_2 КОН_БЛОК_1 КОН_ПРОГ
:prg4_107.asm - программа на ассемблере сортировки Шелла
.data
: задаем массив
masdb 44,55.12.42.94.18,06,67
n=$-mas
X db 0
:задаем массив расстояний
mas_dist db 7.5.3.1
t=$-mas_dist ;t - количество элементов в массиве расстояний
.code
xorbx.bx :в bx - очередное смещение из mas_dist[] :dl
movcx.t :цикл по t (внешний)
movsi.O :индекс по mas_dist[] (?@d2: push ex
mov bl,mas_dist[si] :в bx - очередное смещение из mas_dist[]
inc si push si :ДЛЯ j:=h ДО n-1
mov di.bx ' ;di - это j :j:=h+l - это неявно для нумерации массива с нуля @@d3: cmpdi.n-1 ;j=<n ?
ja @@ml :конец итерации при очередном mas_dist[]
mov si ,di
sub si.bx :i:=j-h: si - это i
mov al ,mas[di] ;x:=mas[j]
movx.al :x:=mas[j] @@d4: :ЕСЛИ Х>= mas[i] TO ПЕРЕЙТИ_НА №й6
mov al,x
cmpal ,mas[si]
jae@@d6
:d5 - mas[i+h]:=mas[i]: i:=i-h push di push si popdi
adddi.bx :i+h
mov al, mas[si] :mas[i+h]:=mas[i]
movmas[di],al :mas[i+h]:=mas[i] pop di
subsi.bx ;i:=i-h
cmpsi.O ;ЕСЛИ i>0 TO ПЕРЕЙТИ_НА @@d4
jg Ш4
@@d6: ;mas[i+h]:=x
push di push si pop di
adddi.bx ;i+h
mov al .x
movmas[di].al ;mas[i+h]:=x popdi
incdi :j:=j+l
jmp ШЗ @@ml: pop si pop ex
loop Ш2 @@exit:
Сортировка с помощью дерева
Следующий алгоритм (программа prgl0_229.asm) является улучшением сортировки прямым выбором. Автор алгоритма сортировки с помощью дерева — Дж. У. Дж. Уильяме (1964 год). В литературе этот алгоритм носит название «пирамидальной» сортировки. Если обсужденные выше сортировки интуитивно понятны, то алгоритм данной сортировки необходимо пояснить подробнее. Этот алгоритм предназначен для сортировки последовательности чисел, которые являются отображением в памяти дерева специальной структуры — пирамиды. Пирамида — помеченное корневое двоичное дерево заданной высоты h, обладающее тремя свойствами:
На Рисунок 2.3 изображено несколько деревьев, из которых лишь одно Т4 является пирамидой.
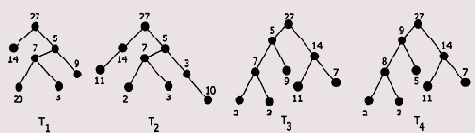
Рисунок 2.3. Примеры деревьев (Т4 — пирамида)
Такая структура пирамид позволяет компактно располагать их в памяти. Например, пирамида, показанная на рисунке, в памяти будет представлена следующим массивом: 27, 9, 14, 8, 5, 11, 7, 2, 3. Оказывается, что такая последовательность чисел легко подвергается сортировке.
Таким образом, сортировка массива в соответствии с алгоритмом пирамидальной сортировки осуществляется в два этапа: на первом этапе массив преобразуется в отображение пирамиды; на втором — осуществляется собственно сортировка. Соответственно нами должны быть разработаны две процедуры для выполнения задач каждого из этих двух этапов.
ПРОЦЕДУРА insert_item_in_tree (i. mas. N) //
//insert_item_in_tree - процедура на псевдоязыке вставки элемента на свое место
в пирамиду //Вход: mas[n] - сформированная не до конца пирамида: 1 - номер добавляемого элемента
в пирамиду из mas[n] (с конца): n - длина пирамиды //Выход:действие - элемент добавлен в пирамиду.
НАЧ_ПРОГ
j:=i @@ml: k:=2*j: h-k+1
ЕСЛИ (1=<N И (mas[j]<mas[k] ИЛИ mas[j]<mas[l]) TO ПЕРЕЙТИ_НА @йп6
ИНАЧЕ ПЕРЕЙТИ_НА @@m2
КОН_ЕСЛИ @@m6: ЕСЛИ tnas[k]>mas[l] TO ПЕРЕЙТИ_НА @@т4
ИНАЧЕ ПЕРЕЙТИ_НА @@тЗ
КОН_ЕСЛИ @@т4: x:=mas[j]
mas[j]:=mas[k]
j:=k
mas[k]:=x ПЕРЕЙТИ_НА (a0ml (а@тЗ: x:=mas[j]
mas[j]:=mas[l]
mas[l]:=x
ПЕРЕЙТИ_НА @@ml*
@@m2: ЕСЛИ (k==n И mas[j]<mas[k]) TO ПЕРЕЙТИ_НА @@m7
ИНАЧЕ ПЕРЕЙТИ_НА @@m8
КОН_ЕСЛИ @@m7: x:=mas[j]
mas[j]:=mas[n]
;m-n/2 - значение, равное половине числа элементов массива mas
push si push ex
movj.si :j\»1 @@m4:
movsi.j :i->si
movax.j :k:=2*j; l:-k+l
shlax.l :j*2
movk.ax : k :=j*2
inc ax
movl.ax :l:»k+l
cmpax.m :l<m
ja @@m2
moval ,raas[si-l] ;ax:-mas[j]
mov di,k
emp al ,mas[di-l]
jna @@m6
inc di
emp al.mas[di-l]
jna @@m6
jmp @@m2
@@m6: ;условие выполнилось:
;2j+l+<M AND (mas[j]<mas[2j] OR mas[j]<mas[2j+l]) :обмен с mas[j]
mov di,k
mov al ,mas[di-1] ;ax:=mas[k]
inc di
emp al,mas[di-l] :mas[k]>mas[l]
jna ШтЗ
mov al ,raas[si-l]
movx.al ;x:=rnas[j]
dec di
mov al ,mas[di-l]
movmas[si-l].al :mas[j]:=mas[k]
movj.di :j:=k
mov al .x
movmas[di-l],al :mas[k]:=x
jmp @?m4
:@@m3: x:=mas[j] ;ПЕРЕЙТИ_НА @@ml №m3: :mas[k] =< mas[l]
mov al,mas[si-l]
movx.al :x:=mas[j]
mov al,mas[di-l]
movmas[si-l].al ;mas[j]:=mas[l]
movj.di :j:=l
mov al ,x
movmas[di-l].al ;mas[l]:=x
jmp @@m4 Шт2: ; условие не выполнилось: 2j+l+<M AND (mas[j]<mas[2j] OR mas[j]<mas[2j+l])
mov ax.k
emp ax.m
Нахождение медианы
Медиана - элемент последовательности, значение которго не больше значений одной половины этой последовательности. Например, медианой последовательности чисел 38 7 5 90 65 8 74 43 2 является 38.
оответствующая отсортированная последовательность будет выглядеть так: 2 5 7 8 38 43 65 74 90.
Задачу нахождения медианы можно решить просто — предварительно отсортировать исходный массив и выбрать средний элемент. Но К. Хоор предлагает метод, который решает задачу нахождения медианы быстрее и соответственно может рассматриваться как вспомогательный для реализации других задач. Достоинство метода К. Хоора заключается в том, что с его помощью можно эффективно находить не только медиану, но и значение k-го по величине элемента последовательности. Например, третьим по величине элементом приведенной выше последовательности будет 7.
Значение k-го элемента массива определяется по формуле k=n/2, где п — длина исходной последовательности чисел.
Ниже приведена программа prg4_123.asm, которая находит элемент-медиану массива. Аналогичную функцию выполняет и процедура median, но процедура отличается тем, что ее можно вызывать динамически во время работы программы, в которой она используется.
ПРОГРАММА prg4_123
//
//prg4_123 - программа на псевдоязыке нахождения k- го по величине элемента массива mas
длиною п. Для нахождения медианы к=п/2. //Вход: mas[n] - неупорядоченная последовательность двоичных значений: к - номер
искомого по величине элемента mas[n]. //Выход: х - значение к-го по величине элемента последовательности mas[n].
// .....
ПЕРЕМЕННЫЕ
INT_BYTE n: ;длина mas[n]
INT_BYTE mas[n]: //сортируемый массив размерностью n (О..n-l)
INTJYTE X:W;i=0: j=0; 1=0; г=0 // j: 1; г - индексы
НАЧПРОГ
1:=1: г:=п ПОКА 1<г ДЕЛАТЬ НАЧ_БЛОК_1 х:=а[к]: 1:=1: j:=r ПОВТОРИТЬ
ПОКА a[i]<x ДЕЛАТЬ i:=i+l ПОКА х< a[j] ДЕЛАТЬ j:=j-l ЕСЛИ i<j TO НАЧ_БЛ0К_2
w:=a[i]: а[1]:-аШ; a[j]:=w i:=i+l: j:=j-l К0Н_БЛ0К_2 ПОКА (i>j) ЕСЛИ j<k TO 1:=I ЕСЛИ k<i T0 r:=j КОН_БЛОК_1 КОН_ПРОГ
;prg4_123 - программа на ассемблере нахождения k-го по величине элемента массива mas длиною п. Для нахождения медианы к=п/2.
.data
jge $+6
movR.di :R<-J :цикл(1)конец jmp @@m8
Быстрая сортировка
Последний рассматриваемый нами алгоритм (программа prglO_223.asm) является улучшенным вариантом сортировки прямым обменом. Этот метод разработан К. Хоором в 1962 году и назван им «быстрой сортировкой». Эффективность быстрой сортировки зависит от степени упорядоченности исходного массива. Для сильно неупорядоченных массивов — это один из лучших методов сортировки. В худшем случае, когда исходный массив почти упорядочен, его быстрая сортировка по эффективности не намного лучше сортировки прямым обменом.
Идея метода быстрой сортировки состоит в следующем. Первоначально среди элементов сортируемого массива mas[l. .n] выбирается один mas[k], относительно которого выполняется переупорядочивание остальных элементов по принципу — элементы mas[i]<mas[k] (i=0. .n-1) помещаются в левую часть mas; элементы mas[i]>mas[k] (i=0. .n-1) помещаются в правую часть mas. Далее процедура повторяется в полученных левой и правой подпоследовательностях и т. д. В конечном итоге исходный массив будет правильно отсортирован. В идеальном случае элемент mas[k] должен являться медианой последовательности, то есть элементом последовательности, значение которого не больше значений одной части и не меньше значений оставшейся части этой последовательности. Нахождению медианы было посвящено обсуждение программ предыдущего раздела. В следующей программе элементом mas[k] является самый левый элемент подпоследовательности.
ПРОГРАММА prg27_136
//prg27_136 (по Кнуту) - программа на псевдоязыке «быстрой сортировки» массива. //Вход: mas[n] - неупорядоченная последовательность двоичных значений длиной п. //Выход: mas[n] -упорядоченная последовательность двоичных значений длиной n.
ПЕРЕМЕННЫЕ
INTJYTE n: //длина mas[n]
INT_BYTE mas[n]; //сортируемый массив размерностью п (О..п-1)
INTJYTE К; TEMP: i=0; j=0: 1=0: г=0; // i. j. 1. г - индексы
INT_WORD M=l //длина подпоследовательности, для которой производится сортировка методом
прямых включений //для отладки возьмем М=1 НАЧ_ПРОГ
ЕСЛИ M<N TO ПЕРЕЙТИ_НА q9
1 :-1: г:=п
ВКЛЮЧИТЬ_В_СТЕК (Offffh) //Offffh - признак пустого стека q2: i :-l: j:-r+l: k:=mas[l] q3: ЕСЛИ i=<j-l TO ПЕРЕЙТИ_НА qq3
ПЕРЕЙТИ_НА q4 //итерация прекращена qq3: i:=i+l
ЕСЛИ mas[i]<K TO ПЕРЕЙТИ_НА q3 q4: j:-j-l
ЕСЛИ j<1 TO ПЕРЕЙТИ_НА q5
ЕСЛИ K<mas[j] TO ПЕРЕЙТИ_НА q4
ЕСЛИ j>i TO ПЕРЕЙТИ_НА q6
Iq2: ;1:-1: j:-r+l: k:-nas[l] movsi.L ;i(si):=L mov di . R incdi ;j(di):=R+l xor ax.ax mov al ,mas[si] mov k.al
q3: :ЕСЛИ 1-sj-l TO ПЕРЕЙТИ_НА qq3 inc si ;i:=i+l cmp si.di :i=<j jleqq3
dec si :сохраняем i=<j jmp q4 :ПЕРЕЙТИ_НА д4//итерация прекращена qq3: moval.k ;i:=i+l
cmpmas[si].al :ЕСЛИ mas[i]<K TO ПЕРЕЙТИ_НА q3
jb q3
q4: decdi ;j:=j-l cmpdi.si :j>=i-l jb q5 mov al ,k :ЕСЛИ K<mas[j] TO ПЕРЕЙТИ_НА q4
cmp al ,mas[di]
»jb q4 q5: ;ЕСЛИ j>i TO ПЕРЕЙТИ_НА q6 cmpdi.si :j=<i ??? J9 q6 movbx.L ://обмен mas[l]:= mas[j] mov dl ,mas[bx] xchg mas[di].dl xchg mas[bx].dl jmpq7 :ПЕРЕЙТИ_НА q7 q6: mov dl.masCsi] ; mas[i]<-> mas[j] xchg mas[di].dl xchg mas[si].dl jmpq3 ;ПЕРЕЙТИ_НА q3 q7: ;ЕСЛИ r-j>j-l>M TO mov ax,г
subax.di ;r-j->ax mov bx.di
subbx.l :j-l->bx cmpax.bx :r-j>j-l ??? jl q7_m4
cmpbx.M ;j-l>M ??? jleq7_m3 ;1, r-j>j-l>M - в стек (j+l.r); r:=j-l; перейти на шаг q2
mov ax.di inc ax push ax
(push г mov r.di dec г :г:=j -1 q7_m4: ;r-j>M ??? cmp ax.M jg q7_m2 cmp bx. M
jleq8 ;4. j-l>M>r-j - r:=j-l: перейти на шаг q2
mov r.di
dec г
jmpq2 q7_m3: cmpax.M
jleq8 ;3. r-j>M>j-l - l:=j+l: перейти на шаг q2
mov 1,di
inc 1
jmpq2 q7_m2: :2. j-l>r-j>M - в стек (l.j-1); l:=j+l; перейти на шаг q2
push 1
mov ax.di
inc ax
push ax
mov 1 ,di
inc 1
jmpq2 q8: извлекаем из стека очередную пару (l.r)
pop г
cmpr.Offffh :ЕСЛИ r<>0ffffh TO ПЕРЕЙТИ_НА q2
je q9
pop!
jmpq2 q9: ;сортировка методом пряных включений - при М=1 этот шаг можно опустить (что и сделано
для экономии места)
Обратите внимание на каскад сравнений шага q7, целью которых является проверка выполнения следующих неравенств:
Проверка этих неравенств реализуется в виде попарных сравнений, последовательность которых выглядит так, как показано на Рисунок 2.4.
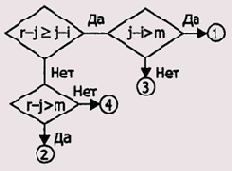
Рисунок 2.4. Последовательность сравнений шага q7
За подробностями алгоритма можно обратиться к тому 3 «Сортировка и поиск» книги Кнута .
Сушествует другой вариант алгоритма этой сортировки — у Вирта в книге «Алгоритмы + структуры данных - программы» [4]. Но у него используется понятие медианы последовательности. Задачу нахождения медианы мы рассматривали выше. Эта задача интересна еще и тем, что она, по сути, является одной из задач поиска, рассмотрению которых посвящен следующий раздел.