CRC-арифметика
CRC-арифметика
Расчеты CRC ведутся в двоичной системе счисления. При проведении CRC-вы-числений используется специальная CRC-арифметика, которая, по сути, является полиномиальной арифметикой по модулю 2. Полиномиальная арифметика по модулю 2 — это еще один из видов арифметик, используемых для решения задач в определенной предметной области и отличающихся от привычной двоичной арифметики с циклическим переносом отсутствием переносов и вычислением всех коэффициентов по модулю 2 . В уроке 20 «ММХ-технология микропроцессоров Intel» учебника при рассмотрении ММХ-команд мы знакомились с одной из таких альтернативных арифметик — арифметикой с насыщением. Теперь рассмотрим особенности CRC-арифметики.
Итак, как отмечено выше, в основе CRC-арифметики лежит полиномиальная арифметика. По определению, полином — линейная комбинация (сумма) произведений целых степеней заданного набора переменных с постоянными коэффициентами. Частный случай — полином, содержащий одну переменную:
u(x)=unxn+...u,x1+uoxo.
Здесь un, nu щ — элементы некоторой алгебраической системы S, называемые коэффициентами; х — переменная полинома, которую можно рассматривать как формальный символ без определенного значения. Алгебраическая система S обычно представляет собой множество целых или рациональных чисел в диапазоне 0..m-1 со сложением, вычитанием и умножением, выполняемыми по модулю т. Для нашего рассмотрения особенно важна полиномиальная арифметика по модулю 2, в которой каждый коэффициент полинома равен одному из двух значений — 0 или 1. Например, шестнадцатеричное значение ОеЗп может быть представлено следующим полиномом:
1х27 + 1х26 + 1х25 + 0х24 + 0х23 + 0х22 + 1x21 + 1x2°.
Если ввести в качестве переменной х=2, то получим следующий двоичный полином:
1хx7 + 1xx6 + 1xx5 + 0хх4 + 0xx3 + 0xx2 + 1xx1 + 1хх°.
В этом полиноме, строго говоря, значение х не играет особой роли, так как данное двоичное число можно представить полиномом в другой системе счисления, например, шестнадцатеричной: ехх1 + 2хх°, где х = 16. При этом заметим, что в том и другом случае цифры 0, 1, е, 2 — это просто цифры двоичной и шестнадцатеричной систем счисления.
Так как слагаемые двоичного полинома с нулевыми коэффициентами не дают никакого вклада в конечный результат, то их можно попросту отбросить, оставив только слагаемые, переменные которых имеют единичные коэффициенты:
1xx7 + 1xx6 + 1xx5 + 0xx4 + 0xx3 + 0xx2 + 1xx1 + 1хх° -
= 1xx7 +1xx6 + lxx5 + 1xx1+ 1xx0 = = x7 + x6 + x5 + x1 + x°.
Здесь x = 2. Над полиномами можно выполнять арифметические операции: сложение, умножение и вычитание. Процессы выполнения этих операций для полиномиальной арифметики и обычной арифметики многократной точности (см. главу 1) похожи. Главное отличие в том, что из-за отсутствия связи между коэффициентами полинома понятие переноса в полиномиальной арифметике отсутствует.
Например, для умножения 7h (0111b) на 5h (0101b) выполняются действия:
(х2 + х1 + х°)х(х2 + х°) = (х4 + х3 + х2 + х2 + х1 + х°) -=х4 + х3 + х2 + х2 + х1 + х° + х°= х4 + х3 + 2х2 + х1 + 2х°.
Для того чтобы получить в ответе 35, мы должны х взять равным 2 и привести коэффициенты у членов полинома 2х° и 2х2 к двоичным, сделав перенос соответствующих единиц в старшие разряды: 01010 переносы 11111 результат
100011 = 35)0.
В результате получим двоичный полином х5+х'+х°.
Эти рассуждения призваны сформулировать очередной тезис о том, что переносы, как и в обычной арифметике, можно выполнять в случае, когда известно основание системы счисления. То есть до тех пор, пока мы не знаем х, мы не можем производить и переносы. В приведенном выше примере, мы не знаем, что 2х2 и 2х° на самом деле являются х3 и х1 до тех пор, пока не известно, что х = 2. То есть в полиномиальной арифметике коэффициенты при разных степенях изолированы друг от друга и отношения между ними не определены. Из-за этого возникает первая странность полиномиальной арифметики — операции сложения и вычитания в ней абсолютно идентичны и вместо них можно смело оставлять одну. Например, сложение по правилам полиномиальной арифметики по модулю 2, будем ее далее называть CRC-арифметикой, будет выполнено так:
| 11111011 | |
| + | 11001010 |
| 00110001 |
Из этого примера видны правила сложения двоичных разрядов в арифметике t с отсутствием переносов:
0+0=0; 0+1 = 1; 1+0=1; 1 + 1=0.
Операцию вычитания демонстрирует следующий пример:
| 11111011 | |
| - | 11001010 |
| 00110001 |
0-0=0; 0-1=1; 1-0=1; 1-1=0.
Сравнение примеров для сложения и вычитания полиномов по модулю 2, а также правил, по которым они выполняются, показывает то, что эти две операции CRC-арифметики идентичны и по принципу формирования результата они аналогичны команде ассемблера XOR. Цель, которой достигают всеми этими условностями, — исключить из поля внимания все величины (путем заемов/перено-сов), лежащие за границей старшего разряда.
Умножение в арифметике с отсутствием переносов также выполняется с учетом особенностей CRC-сложения:
| 1101 | |||
| x | 1011 ----- |
||
| 1101 | |||
| 1101 | |||
| 0000 | |||
| 1101 | |||
| 1111111 |
Для нашего рассмотрения особый интерес представляет операция деления, так как в основе любого алгоритма вычисления CRC лежит представление исходного сообщения в виде огромного двоичного числа, делении его на другое двоичное число и использовании остатка от этого деления в качестве значения CRC. Деление — самая сложная из операций CRC-арифметики. Здесь необходимо ввести так называемое слабое понятие размерности: число X больше или равно числу Y, если оба числа имеют одинаковую размерность и позиции их старших битов единичны, то есть соотношение остальных битов X и Y для операции сравнения не имеет значения. Рассмотрим примеры операции деления, причем для лучшего понимания сделаем это в двух вариантах: вначале вспомним, как выполняется обычное деление (по правилам двоичной арифметики с циклическим переносом), а затем выполним собственно CRC-деление.
Возьмем произвольную двоичную последовательность и разделим ее на некоторое число по правилам двоичной арифметики с циклическим переносом
(Рисунок 9.3).
По правилам CRC-арифметики деление для приведенных выше исходных данных даст следующий результат (Рисунок 9.4).
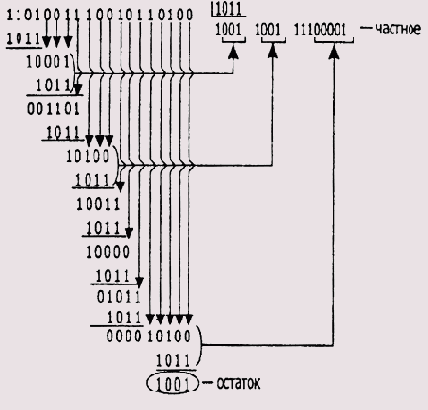
Рисунок 9.3. Схема вычисления двоичного деления (с циклическим переносом)
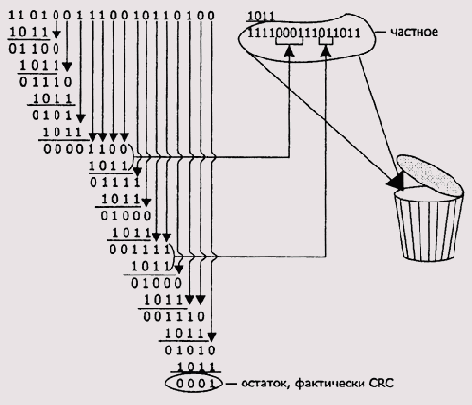
Рисунок 9.4. Схема вычисления CRC-деления
Как видите, результаты обычного и CRC-делений отличаются. Главное, чтобы вы подметили особенность выполнения CRC-деления. Особое внимание обратите на порядок формирования промежуточных результатов в процессе деления. Снос двоичных разрядов из делимого продолжается до тех пор, пока размерности промежуточного битового значения и делителя не сравняются, а их старшие разряды не станут равными 1. После этого над двоичными разрядами выполняется побитовое CRC-вычитание. Соотношение разрядов не важно, главное — это одинаковая размерность и единичные старшие биты. В этом случае считается, что вычитаемое больше вычитаемого, что влечет за собой включение 1 в частное и выполнение операции CRC-вычитания. Это как раз и есть проявление слабого
понятия размерности. Корзина для мусора, показанная на Рисунок 9.4, означает тот факт, что частное для процесса вычисления CRC-битовой последовательности не имеет никакого значения.
Реальные двоичные последовательности являются результатом сцепления порой огромного количества отдельных байтов (символов), образуя одно большое двоичное число, для представления которого нужно использовать двоичные полиномы огромных степеней. При этом каждый бит в подобной последовательности произвольной длины представляется в виде коэффициента длинного полинома. Например, для представления 128-разрядного блока необходим полином, состоящий из 1024 слагаемых, а для 1024-битного блока необходим полином уже с 8192 слагаемыми. В терминах полиномиальной арифметики двоичное число, сформированное в результате подобной сцепки составляющих блока данных, называется полиномом данных {сообщения) и обозначается как D(x) [5, 44]. В алгоритме вычисления CRC вводится еще несколько полиномов и соотношений между ними:
Между перечисленными полиномами существуют следующие отношения:
D(x)=Q(x)xG(x)+R(x), Q(x)=(D(x)-R(x))/G(x).
Эти соотношения приводят к следующим основополагающим для дальнейшего рассмотрения тезисам:
Из приведенного выше описания общей схемы вычисления CRC возникает ряд вопросов: что представляет собой этот магический делитель G(x), каков его размер? Выбор порождающего полинома G(x) — достаточно сложная задача. Перечислим некоторые важные свойства, которые должны учитываться при этом.
Для большинства алгоритмов вычисления CRC значение порождающего полинома известно заранее и, более того, утверждено соответствующими стандартами. Поэтому программисту без особой надобности не стоит терять времени и сил на изобретение нового значения порождающего полинома G(x). Приведем значения некоторых широко известных полиномов, используемых на практике.
Ш х16+х|5+х2+х° — полином 8005h, используемый в протоколе двоичной синхронной передачи фирмы IBM. Он также стандартизован в приложении А «Процедура коррекции ошибок для оконечного оборудования линии с использованием асинхронно-синхронного преобразования» к стандарту V.42 МККТТ. Этот же полином широко известен как полином, используемый в алгоритме вычисления CRC — CRC16.
В заключение отметим, почему выгодно увеличивать число разрядов CRC. Выше уже было отмечено, что алгоритм вычисления CRC по сути своей является одним из возможных (и неплохих) алгоритмов хэширования. Разрядность порождающего полинома G(x) 16 бит обеспечивает до 65 535 значений хэш-функции. Увеличение разрядности полинома G(x) до 32 битов приводит к расширению набора значений хэш-функции уже до 4 294 967 295.
С полиномом связано еще одно понятие — степени полинома, которое по определению является номером позиции его старшего единичного бита (считая с нуля). Например, для полинома 1011 из приведенного выше примера (см. Рисунок 9.4) степень равна 3.
В качестве выводов отметим, что CRC-арифметика отличается от двоичной отсутствием переносов/заемов, а CRC-вычитание и сложение выполняются по
тем же правилам, что и команда ассемблера XOR, что и обусловливает ее важную роль при вычислении значений CRC.